Crystallographic point group
In crystallography, a crystallographic point group is a set of symmetry operations, like rotations or reflections, that leave a central point fixed while moving other directions and faces of the crystal to the positions of features of the same kind. For a true crystal (as opposed to a quasicrystal), the group must also be consistent with maintenance of the three-dimensional translational symmetry that defines crystallinity. The macroscopic properties of a crystal would look exactly the same before and after any of the operations in its point group. In the classification of crystals, each point group is also known as a crystal class.
There are infinitely many three-dimensional point groups; However, the crystallographic restriction of the infinite families of general point groups results in there being only 32 crystallographic point groups. These 32 point groups are one-and-the same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.
The point group of a crystal, among other things, determines directional variation of the physical properties that arise from its structure, including optical properties such as whether it is birefringent, or whether it shows the Pockels effect.
Contents |
Notation
The point groups are denoted by their component symmetries. There are a few standard notations used by crystallographers, mineralogists, and physicists.
For the correspondence of the two systems below, see crystal system.
Schoenflies notation
In Schoenflies notation, point groups are denoted by a letter symbol with a subscript. The symbols used in crystallography mean the following:
- Cn (for cyclic) indicates that the group has an n-fold rotation axis. Cnh is Cn with the addition of a mirror (reflection) plane perpendicular to the axis of rotation. Cnv is Cn with the addition of a mirror plane parallel to the axis of rotation.
- S2n (for Spiegel, German for mirror) denotes a group that contains only a 2n-fold rotation-reflection axis.
- Dn (for dihedral, or two-sided) indicates that the group has an n-fold rotation axis plus a twofold axis perpendicular to that axis. Dnh has, in addition, a mirror plane perpendicular to the n-fold axis. Dnd has, in addition to the elements of Dn, mirror planes parallel to the n-fold axis.
- The letter T (for tetrahedron) indicates that the group has the symmetry of a tetrahedron. Td includes improper rotation operations, T excludes improper rotation operations, and Th is T with the addition of an inversion.
- The letter O (for octahedron) indicates that the group has the symmetry of an octahedron (or cube), with (Oh) or without (O) improper operations (those that change handedness).
Due to the crystallographic restriction theorem, n = 1, 2, 3, 4, or 6 in 2- or 3-dimensional space.
| n | 1 | 2 | 3 | 4 | 6 |
|---|---|---|---|---|---|
| Cn | C1 | C2 | C3 | C4 | C6 |
| Cnv | C1v=C1h | C2v | C3v | C4v | C6v |
| Cnh | C1h | C2h | C3h | C4h | C6h |
| Dn | D1=C2 | D2 | D3 | D4 | D6 |
| Dnh | D1h=C2v | D2h | D3h | D4h | D6h |
| Dnd | D1d=C2h | D2d | D3d | D4d | D6d |
| S2n | S2 | S4 | S6 | S8 | S12 |
D4d and D6d are actually forbidden because they contain improper rotations with n=8 and 12 respectively. The 27 point groups in the table plus T, Td, Th, O and Oh constitute 32 crystallographic point groups
Hermann–Mauguin notation
An abbreviated form of the Hermann–Mauguin notation commonly used for space groups also serves to describe crystallographic point groups. Group names are
| 1 | 1 | |||||
| 2 | 2⁄m | 222 | m | mm2 | mmm | |
| 3 | 3 | 32 | 3m | 3m | ||
| 4 | 4 | 4⁄m | 422 | 4mm | 42m | 4⁄mmm |
| 6 | 6 | 6⁄m | 622 | 6mm | 62m | 6⁄mmm |
| 23 | m3 | 432 | 43m | m3m |
The correspondence between different notations
| Crystal family | Crystal system | Hermann-Mauguin (full symbol) |
Hermann-Mauguin (short symbol) |
Shubnikov[1] | Schoenflies | Orbifold | Coxeter | Order |
|---|---|---|---|---|---|---|---|---|
|
|
1 | 1 | 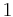 |
C1 | 11 | [ ]+ | 1 | |
| 1 | 1 | 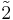 |
Ci = S2 | x | [1+,2+] | 2 | ||
|
|
2 | 2 | 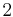 |
C2 | 22 | [2]+ | 2 | |
| m | m | 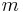 |
Cs = C1h | * | [ ] | 2 | ||
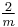 |
2/m | 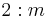 |
C2h | 2* | [2,2+] | 4 | ||
|
|
222 | 222 | 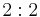 |
D2 = V | 222 | [2,2]+ | 4 | |
| mm2 | mm2 | 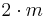 |
C2v | *22 | [2] | 4 | ||
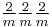 |
mmm | 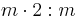 |
D2h | *222 | [2,2] | 8 | ||
|
|
4 | 4 | 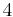 |
C4 | 44 | [4]+ | 4 | |
| 4 | 4 | 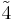 |
S4 | 2x | [2+,4+] | 4 | ||
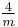 |
4/m | 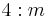 |
C4h | 4* | [2,4+] | 8 | ||
| 422 | 422 | 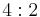 |
D4 | 422 | [4,2]+ | 8 | ||
| 4mm | 4mm | 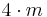 |
C4v | *44 | [4] | 8 | ||
| 42m | 42m | 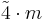 |
D2d | 2*2 | [2+,4] | 8 | ||
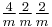 |
4/mmm | 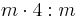 |
D4h | *422 | [4,2] | 16 | ||
|
|
|
3 | 3 | 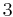 |
C3 | 33 | [3]+ | 3 |
| 3 | 3 | 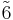 |
S6 = C3i | 3x | [2+,6+] | 6 | ||
| 32 | 32 | 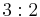 |
D3 | 322 | [3,2]+ | 6 | ||
| 3m | 3m | 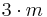 |
C3v | *33 | [3] | 6 | ||
3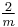 |
3m | 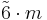 |
D3d | 2*3 | [2+,6] | 12 | ||
|
|
6 | 6 | 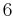 |
C6 | 66 | [6]+ | 6 | |
| 6 | 6 | 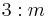 |
C3h | 3* | [2,3+] | 6 | ||
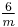 |
6/m | 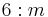 |
C6h | 6* | [2,6+] | 12 | ||
| 622 | 622 | 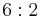 |
D6 | 622 | [6,2]+ | 12 | ||
| 6mm | 6mm | 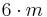 |
C6v | *66 | [6] | 12 | ||
| 6m2 | 6m2 | 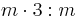 |
D3h | *322 | [3,2] | 12 | ||
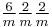 |
6/mmm | 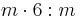 |
D6h | *622 | [6,2] | 24 | ||
|
|
23 | 23 | 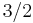 |
T | 332 | [3,3]+ | 12 | |
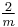 3 3 |
m3 | 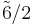 |
Th | 3*2 | [3+,4] | 24 | ||
| 432 | 432 | 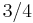 |
O | 432 | [4,3]+ | 24 | ||
| 43m | 43m | 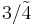 |
Td | *332 | [3,3] | 24 | ||
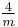 3 3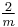 |
m3m | 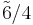 |
Oh | *432 | [4,3] | 48 | ||